

(We'll just run the commands over)įinally,we perform elementary row operations until our matrix is in reduced row echelon form.Īgain, let's check that this is actually the inverse.Īside from these roundoff errors, we get the identity matrix! We can do this again with another randomly selected 3x3 matrix.
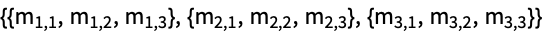
You can see that they are essentially zero. The numbers off the diagonal which look nonzero are just roundoff error. That is to say, when I multiply A and AInv I should get the identity matrix. Later on when we talk about matrix multiplication we'll see that the inverse we've just calculated is the multiplicative inverse of A. Since the left hand side is the identity matrix,the right hand side is the inverse of our matrix. RowReduce is the function Mathematica uses to put a matrix in reduced row echelon form.

It takes some work to get Mathematica to do this, but you shouldn't worry about that.įinally,we perform elementary row operations until our matrix is in reduced row echelon form. Now we augment the matrix A with the identity matrix. The procedure I've written to generate a random matrix gives an n x n matrix with entries selected randomly between 0 and 1. We start by selecting a random 3x3 matrix which we'll call A. I want to implement the procedure for calculating the inverse of an operator which we talked about in class. You don't need to see these, but they will generate the random matrices I'll use in my computations. Computing the Inverse of a Matrix via Row Reduction


 0 kommentar(er)
0 kommentar(er)
